el circulo

CIRCULO

Un círculo, en geometría, es el lugar geometrico de los ountos del plano cuya distancia a otro punto fijo, llamado centro, es menor o igual que una cantidad constante, llamada radio. En otras palabras, es la región del plano delimitada por una circunferencia y que posee un área definida.

En castellano, la palabra círculo tiene varias acepciones, y se utiliza indistintamente círculo por circunferencia, que es la curva geométrica plana, cerrada, cuyos puntos son equidistantes del centro, y sólo posee longitud (es decir, el perímetro del círculo). "Aunque ambos conceptos están relacionados, no debe confundirse la circunferencia (línea curva) con el círculo (superficie).

CARACTERISTICAS

Perímetro del Círculo

El perímetro de un círculo es una circunferencia y su ecuación es:

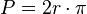(en función del radio).

o

(en función del diámetro).

donde es el perímetro, es la constante matemática pi (), es el radio y es el diámetro del círculo.

Área del círculo

 Existen numerosas fórmulas para calcular el área de un círculo. Un círculo de radio , tendrá un área

 ; en función del radio (r).

o

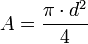; en función del diámetro (d), pues

o

; en función de la longitud de la circunferencia máxima (C),

pues la longitud de dicha circunferencia es:

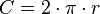
Área del círculo como superficie interior del polígono de infinitos lados

 

El área de un círculo se deduce sabiendo que la superficie interior de cualquier polígono regular es igual al producto entre el apotema y el  perimetro de este poigono es decir: .

Si se considera la circunferencia como el polígono regular de infinitos lados, entonces el apotema coincide con el radio de la circunferencia y el perímetro con la longitud de la circunferencia. Por tanto el área interior es: