Una circunferencia es el lugar geométrico de los puntos de un plano que equidistan de otro punto fijo y coplanario llamado centro en una cantidad constante llamada radio.
A la distancia entre cualquiera de sus puntos y el centro se le denomina radio. El segmento de recta formado por dos radios alineados se llama diámetro. Es la mayor distancia posible entre dos puntos que pertenezcan a la circunferencia. La longitud del diámetro es el doble de la longitud del radio. La circunferencia sólo posee longitud. Se distingue del círculo en que éste es el lugar geométrico de los puntos contenidos en una circunferencia determinada; es decir, la circunferencia es el perímetro del círculo cuya superficie contiene.
Puede ser considerada como una elipse de excentricidad nula, o una elipse cuyos semiejes son iguales. También se puede describir como la sección, perpendicular al eje, de una superficie cónica o cilíndrica, o como un polígono de infinitos lados, cuya apotema coincide con su radio.
La circunferencia de centro en el origen de coordenadas y radio 1 se denomina circunferencia unidad o circunferencia goniométrica
Elementos de la circunferencia
Existen varios puntos, rectas y
segmentos, singulares en la circunferencia:
- Centro, el punto interior equidistante de todos los puntos de la circunferencia;
- Radio, el segmento que une el centro con un punto cualquiera de la circunferencia;
- Diámetro, el mayor segmento que une dos puntos de la circunferencia (necesariamente pasa por el centro);
- Cuerda, el segmento que une dos puntos de la circunferencia; (las cuerdas de longitud máxima son los diámetros)
- Recta Secante, la que corta a la circunferencia en dos puntos;
- Recta Tangente o simplemente Tangente, la que toca a la circunferencia en un sólo punto;
- Punto de tangencia, el de contacto de la recta tangente con la circunferencia;
- arco, el segmento curvilíneo de puntos pertenecientes a la circunferencia;
- Semicircunferencia, cada uno de los dos arcos delimitados por los extremos de un diámetro.
diana dominguez, Creado con GeoGebra


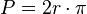 (en función del radio).
(en función del radio). (en función del diámetro).
(en función del diámetro). , tendrá un área
, tendrá un área ; en función del radio (r).
; en función del radio (r).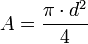 ; en función del diámetro (d), pues
; en función del diámetro (d), pues 
 ; en función de la longitud de la circunferencia máxima (C),
; en función de la longitud de la circunferencia máxima (C),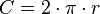
 .
.